Challenge 1: Value-Based Scheduling

Value-Based Scheduling

Most scheduling tools schedule with time - when you create a schedule, whether it's using CPM, resource levelling, or some other algorithm, the objective is to create a fast schedule.

Value-based scheduling is different - you are not looking for fast, you are looking for best value. This can be slow, cheap, and late benefits; it can be fast, expensive and early benefits.

This can be challenging to do, as you are looking at lots of things at once.

• CPM looks only at time - activities have relationships with each other that determine when in time they can be scheduled
• Resource-based optimisers include resources in this - activities still have relationships with each other, but also have resource requirements. Resources will have limits, and you cannot schedule activities if sufficient resources are not available.

There are actually many more decisions to be made than just these. The key ones are:

• Activity Modes: How to execute each activity - do you increase the resource allocation, reduce duration, and accelerate? Do you increase the duration, and thus reduce the demand on resources?
• Resource Modes: How many resources to have available - some resources are easy to flex up and down, and some are not. You may want to invest in hiring an additional piece of equipment like a crane, and this may have substantial set-up costs. You may want to mobilise another specialist crew, and they might need a couple of weeks to mobilise and de-mobilise.

The Project

We've created an example schedule, designed to be quite small and simple (248 activities, 13 resources) but with interesting trade-offs between these factors.

• There are around 100 activities that have Activity Modes. These activities can be accelerated (at the cost of a lower productivity), or slowed down.
• All resources have Resource Modes. You can increase the limit on any resource, by paying the cost of 4 weeks of resource use (2 weeks for mobilisation, 2 weeks for demobilisation). Each resource has a cost per hour of use.
• The faster you complete the project, the earlier the benefits and the lower the overheads. This is all wrapped up into a resource assigned to the LOE activity tracking project duration.

There's no easy solution to this! If you accelerate every activity, the additional costs will outweigh the benefit of finishing early, and overall value will be lower. If you slow everything down, the saving on resource levels will not be enough to cover the cost of finishing later. You need to balance all the choices together - where to invest in additional resources, where to pay for acceleration, where to save by slowing down.

The Rules

Constraints and Modes

1. Prerequisite logic in the XER

   The activity network specified in the XER must be respected.

2. Activity modes

   Only activities under Construction and Commissioning level-2 WBS (MP1.Construction, MP1.Commissioning) can have Activity Modes applied.

   There are 3 Activity Modes. All activities in the XER we provide are specified in "Standard" mode.

   Mode	Duration	Resources
   Slow	200% of Standard	50% units/time
   Standard	No change	No change
   Accelerated	50% of Standard	240% units/time (+20% total hours)

3. Resource modes

   There are baseline resource limits in the XER file, however these are not fixed. Any level may be set for any resource, with the exception of the "Project overhead" resource which must always have a limit of 1 unit/hr.

Valuing a Solution

There are 3 components to the value of a schedule: resources used to execute each activity, project overheads, and resource mobilisation.

All these values are costs, so for each lower is better. The best schedule will have the lowest cost.

1. Activity-level resource use: Based on the Activity Mode selected for each activity, there will be resource assignments with the units/hour and the total units required. Accelerated activities will have a higher total units than Standard or Slow activities. Cost is the sum of the cost of all resource assignments.
2. Project overheads: The project overheads and early (late) delivery value are tracked by the activity "Project overheads". This activity has a single resource assignment with a fixed usage rate of 1 unit/hour.
3. Resource mobilisation: The peak use of each resource is used to calculate the mobilisation (2 weeks) and demobilisation costs (2 weeks). For each resource, the total cost is: Peak resource use (in units) × cost/unit/hour × (40 hours/week × 4 weeks)

PlanLab Solution

Intuition

Schedule optimisation is mathematically very complicated, but the trade-offs you are managing are actually very intuitive. Putting together the jigsaw in the best way is very hard, but how to think about a good solution can be quite simple.

In this case we are trading 3 things against each other: duration, resource mobilisation, and activity acceleration.

• If you accelerate activities, this will require more resource mobilisation and reduce duration
• If you increase resource mobilisation, you can do more activities in parallel, and reduce duration

The Solution Space

These scheduling problems have a massive number of possible solutions. We have 12 resources that we can vary the limits on, and about 100 activities we can choose to accelerate. There's no way to run a search on all the combinations (if you assume there're only 2 settings for each resource, you still have ~10⁵¹ combinations of resource-limits and activity-modes. There are 10¹⁶ seconds in a billion years…)

So we know how we expect the different levers we have (resource limits, activity acceleration) to impact the value, but we don't really have any way to find the right choices for these levers.

Searching for Solutions

The choices we are making can be grouped into resource-decisions and activity-decisions:

• Resource-decisions: how many of each resource to mobilise
• Activity-decisions: what mode to use for each activity, and the scheduled dates for them

We can think about searching for the right activity-decisions, given a set of resource-decisions. This is quite intuitive, as if there're more resources available the choices for activities need to change to make best use of this.

It is possible to try and search for the right combinations by hand, e.g.

• Look at the resource use, and find the resources that are delaying delivery
• Increase the mobilisation of these resources
• Look for the best activity choices (modes and dates) within this

Even for a schedule as small as this, it's likely very hard to do more than a few iterations of this by hand. This kind of search task is ideally suited to automation - hundreds or thousands of potential solutions can be searched every minute.

Our Solution

The best solution we found is £107.5m in cost. The solution achieves a pretty quick delivery (2025-12-23) with controlled resource levels, choosing to accelerate 20 activities and slow down 11.

Arriving at the Solution

The algo does the heavy lifting here, searching through possible solutions in the two steps we identified:

• Making choices for the resource-decisions
• Fine-tuning the activity-decisions for this

If we look at how this search unfolds, we can see this in action! A quick explanation of the plots below:

• Each iteration is the solution generated by one set of decisions (both resource and activity)
• The total cost is broken down into Activity Mode costs, Duration costs and Mobilisation costs.

One Round of Searching

In a round of searching, some resource-choices are explored, and the best activity-choices for these are found. Repeating this creates a wave-like pattern in the total costs. This makes sense intuitively: if you change the resource choices, then what used to be a good set of activity choices are now pretty bad, and total cost will be high until you find good activity choices.

You can see this below - here we have 3 search rounds, where the initial search is within the resource-choices, and then resources stabilise while activity-choices are made. The top chart is Mobilisation Costs, and the lower chart Total Costs.

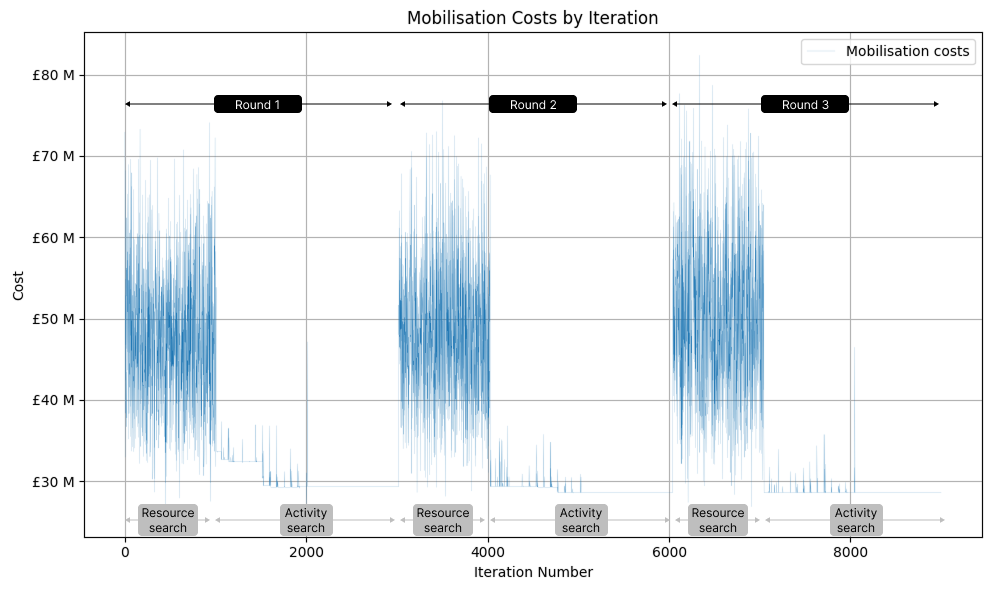
Resource choices exploration - mobilisation costs varying as different resource levels are tested

Total costs across iterations showing the wave-like pattern as resource and activity choices are refined

Lots of Rounds of Searching

If we keep track of the best solution found as we search, then we see how the overall solution is evolving. What is interesting is that the total cost of Activity Modes is very stable → not many changes are being made here, so it is likely that there are some very obviously valuable choices to make here, that are good almost all the time (if you look in more detail at the schedule, you'll see that accelerating some Commissioning activities is very attractive). The difficult activity-choices will be the sequence of execution.

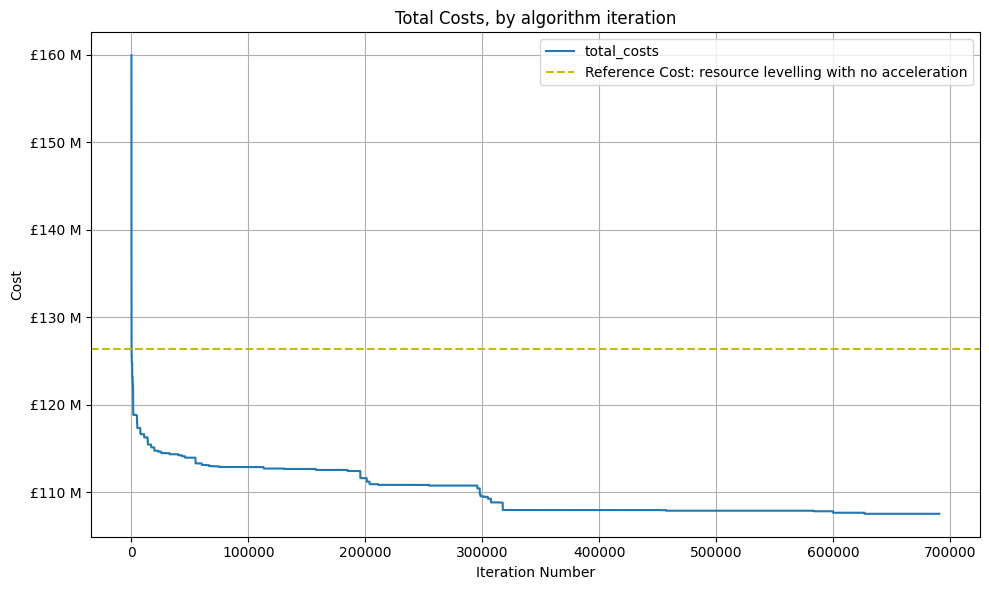
Activity mode costs remain stable - the obvious acceleration choices are consistent winners

Duration costs gradually decrease as better activity sequencing is found

A lot of improvement is made very quickly - if we take the reference cost as a resource-levelled base schedule (~£125m cost), we drop to about £115m within about 10,000 iterations (3 or 4 search rounds). We then have a gradual improvement in the solution, down to £107m at the end.

We see an interesting point at about 300,000 iterations, or 100 search rounds, where a good set of choices were found. Digging a bit more, we can see that this coincides with changes to the resource choices:

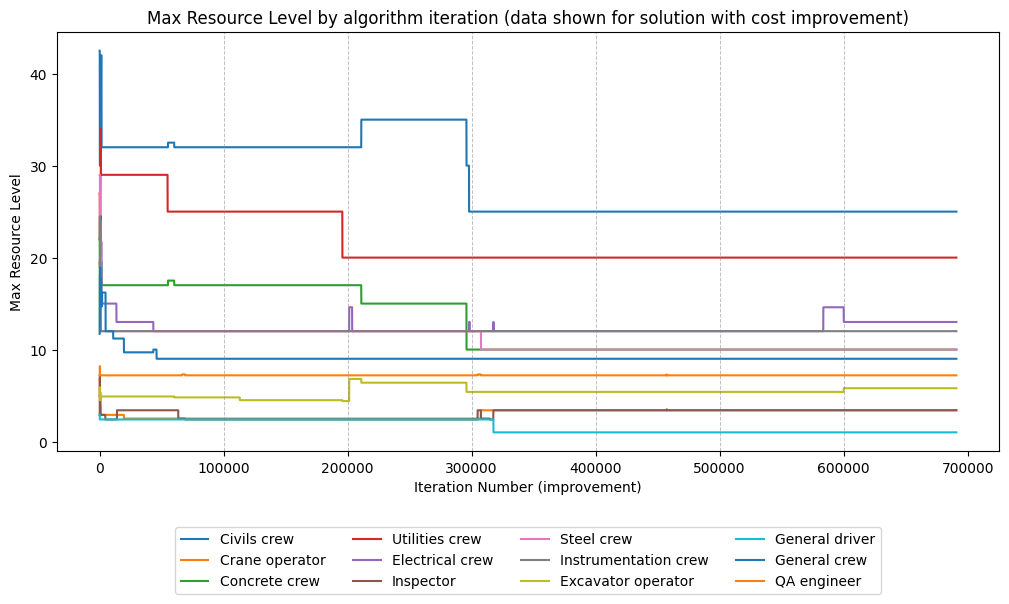
Resource choices over time - note the dramatic fall in Civils Crews at ~300,000 iterations

Here we can see that the number of Civils Crews falls dramatically at this point, but there are slight increases in less-utilised resources at the bottom of the chart - matching this with the Project duration cost, it shows that it was possible to combine these new resource choices with activity choices to find a lower-resource but similar duration solution.

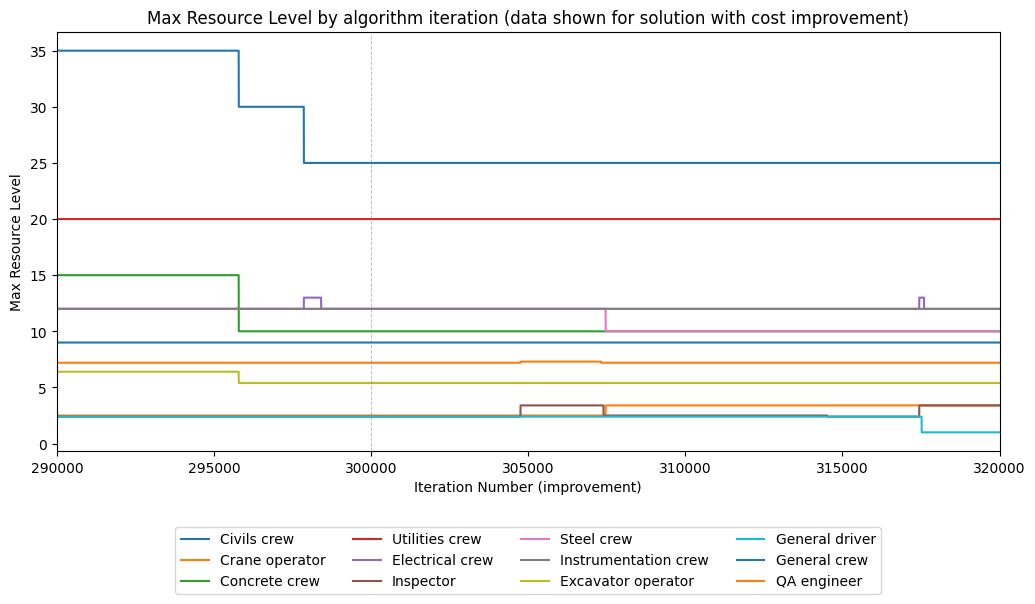
Zooming in on this period - small increases in other resources offset the reduced Civils Crews

Finding Even Better Solutions

It's probable that searching for longer would yield better results, and it's also likely that if we fine-tuned the search algo for just this problem, we could also achieve slightly lower cost solutions (and find them faster).

Having an approach that works well on a broad range of problems is very useful, as we won't have the time to fine-tune algorithms for every individual schedule we see (although for some projects, I'm sure it's worth it!)